Fork me on GitHub

home | news | discuss | issues | license

LURE: range

range : simple discretiation

tim@menzies.us
August, 2017

Use this code to find "natural ranges" in a list of numbers t. Such ranges can be visualized of as a small number of straight lines approximating a cumulative distribution function.

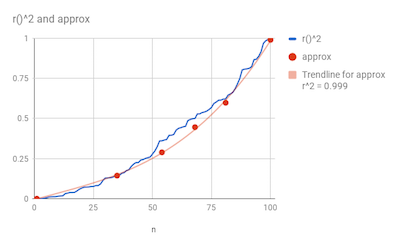
For example, consider a random number function R and 100 numbers drawn from square(R). The following code would propose breaks in that range at (0,0), (36,0.14), (55,0.3), (67,0.47), (80,0.6), (100,1) which looks like this:

Note that a line drawn through our breaks is a good approximation of the original curve. There are two benefits in using this approximation:

  • We no longer need to use, or report, the entire curve. Instead, we can just break up the reasoning into a few bins.
  • Any subsequent supervised discretisation need not reason about the whole curve. Instead, that supervised discretizer needs only to decide which of the breaks found by the unsupervised discretizer need to be combined together.

In the literature, finding such ranges ins called discretisation. A common division of discretisation methods is

  • Supervised: using changes in the dependent variable to decide where to declare a break in some independent variable;
    • For supervised discretisation, see super.lua.
  • Unsupervised: just reflect on each independent variable in isolation. Two common unsupervised methods are
    • EWD: Equal width discretisation; i.e. (max-min)/b to generate, say, b=10 bins
    • EFD: Equal frequency discretisation i.e. divide the numbers according to percentiles says (e.g.) lower, middle, upper third of the numbers

This code is EFD, with some extras to avoid common problems. For example, consider a 33 percent split on the following numbers. Note that the first and second bin would contain the same numbers-- which is odd since you'd expect different bins to be, well, different. 

  1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,
  1,1,1,1,1,1,1,1,2,3,4,5,6,7,8,9

This code builds ranges that at least the size of the equal frequency division. But it fuses one range to the next if they do not have different values.

Input

  • t (mandatory) is a list of items.
  • f (optional) is a function that can extract numbers out of items in t (defaults to returning the whole item). This is very useful for generating ranges from, say, the ages of a list of employees.

Output

Returns a list of ranges, which is a structure containing

  • .n : the number of items form t that fall into this range;
  • ._all : a sample of the numbers in this range;
  • .hi: the highest number in this range;
  • .lo: the lowest number in this range; .span: The span is.hi - .lo`.

The numbers in the input list t are broken such that

  • no range contains too few numbers (controlled by the.chop.m)
  • each range is different to the next one by some epsilon value (controlled by the.chop.cohen).
  • the span of the range (hi - lo) is greater than some enough value (controlled by the.chop.cohen).

Example usage

RANGE=require "range"
R=require "random"

local tmp={}
for x=1,1000 do
  tmp[#tmp+1] = R.r()^2 end
for i,r in pairs(RANGE(tmp)) do
  print(i, r.n, r.lo, r.hi) end

Configuration

  • the.chop.cohen: epsilon = sdOfnums*cohen. If set larger, then the number of ranges will decrease
  • the.chop.m: enough = length(t)^m. If set larger, the number of ranges will decrease
  • the.sample.most: controls how many samples are kept per range. If set smaller, then ranges uses less memory.
 
require "show"
local the=require "config"
local NUM=require "num"
local SOME=require "sample"

Initialize a range

 
local function create() return {
  _all= SOME.create(),
  n  = 0,
  hi = -2^63,
  lo =  2^63,
  span = 2^64} end

Update range i with some numeric x found from within one. Note that, for efficiency sake, we only keep SOME numbers (not all of them). 

local function update(i,one, x)
  if x ~= the.ignore then
    SOME.update(i._all, one)
    i.n = i.n + 1
    if x > i.hi then i.hi = x  end
    if x < i.lo then i.lo = x  end
    i.span = i.hi - i.lo
    return x end  end

Update range manager i with a new range i.now. Push that range onto the list of all ranges i.ranges.

 
local function nextRange(i) 
  i.now  = create()
  i.ranges[#i.ranges+1] = i.now end

Initialize the control parameters for range generation

 
local function rangeManager(t, x)  
  local _ = { 
    x     = x,
    cohen = the.chop.cohen,
    m     = the.chop.m,
    size  = #t,
    ranges= {} -- list of all known ranges 
  }
  nextRange(_)
  _.num = NUM.updates(t, _.x)
  _.hi  = _.num.hi

Any range holding less than enough items is ignored.

 
  _._.enough = _.size^_.m

Any range whose span is less than epsilon is ignored.

 
  _._.epsilon= _.num.sd * _.cohen
  return _ end

Return a function that

  • Sorts a t of items according to the values found by the function x.
  • Then divides that sort into ranges of size of at least enough which break the t into items of at least epsilon in size.
 
return function (t, x,       last)
  x= x or function (z) return z end -- _x_ defaults to the identity
  table.sort(t, function (z1,z2) 
                    local one,two=x(z1),x(z2)
                    return one ~=the.ignore and 
                           two ~=the.ignore and 
                           one < two end )
  local i= rangeManager(t, x)
  for j,one in pairs(t) do
    local x1 = x(one)
    if x1 ~= the.ignore then
      update(i.now, one, x1)
      if j > 1 and
         x1 > last and
         i.now.n       > i.enough  and
         i.now.span    > i.epsilon and

These last two tests are important: they stop the final range being too small

 
         i.num.n - j   > i.enough  and
         i.num.hi - x1 > i.epsilon 
      then nextRange(i) end 
      last = x1  end end
  return i.ranges end

Legal

LURE, Copyright (c) 2017, Tim Menzies All rights reserved, BSD 3-Clause License

Redistribution and use in source and binary forms, with or without modification, are permitted provided that the following conditions are met:

  • Redistributions of source code must retain the above copyright notice, this list of conditions and the following disclaimer.
  • Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution.
  • Neither the name of the copyright holder nor the names of its contributors may be used to endorse or promote products derived from this software without specific prior written permission.

THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT HOLDER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.